Instruction types

There are 204 instructions in the SPU Instruction Set Architecture , and they are grouped into 11 classes according to their functionality.

These instruction classes are shown in Table 1.

Table 1. SPU Instruction Types
Type	Number
Memory Load and Store	16
Constant Formation	6
Integer and Logical Operations	59
Shift and Rotate	31
Compare, Branch, and Halt	40
Hint-for-Branch	3
Floating-Point	28
Control	8
SPU Channel	3
SPU Interrupt Facility	7
Synchronization and Ordering	3

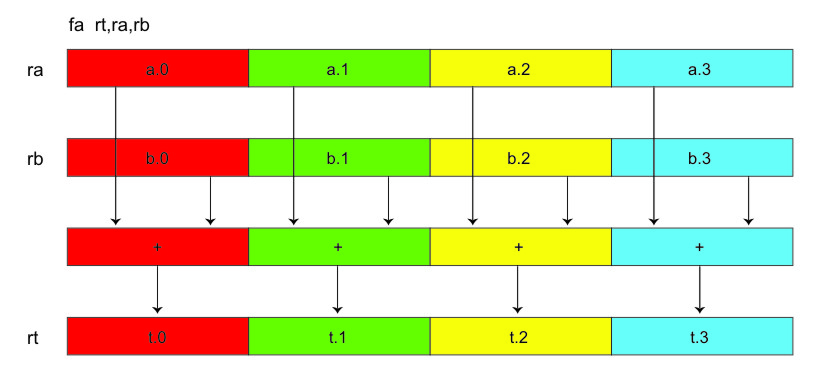
Figure 1 shows one example of an SPU SIMD instruction — the floating-point add instruction, fa. This instruction simultaneously adds four pairs of floating-point vector elements, stored in registers ra and rb, and produces four floating-point results, written to register rt.

Figure 1. SIMD floating-point Add instruction function

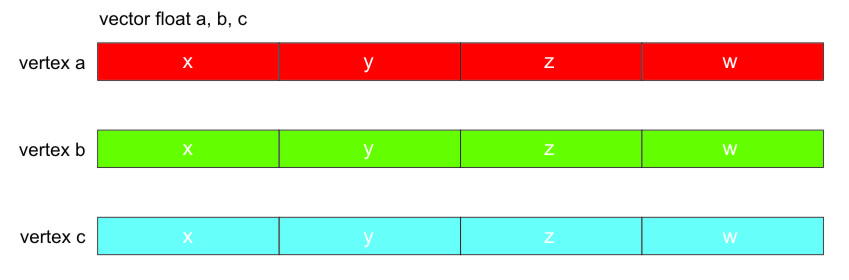
Depending on the programmer's performance requirements and code size restraints, advantages can be gained by properly grouping data in an SIMD vector. Figure 2 shows a natural way of using SIMD vectors to store the homogenous data values (x, y, z, w) for the three vertices (a, b, c) of a triangle in a 3D-graphics application. This arrangement is called an array of structures (AOS), because the data values for each vertex are organized in a single structure, and the set of all such structures (vertices) is an array.

Figure 2. Array-of-structures data organization for one triangle

The data-packing approach that is shown in Figure 2 often produces small code sizes, but it typically executes poorly and generally requires significant loop-unrolling to improve its efficiency. If the vertices contain fewer components than the SIMD vector can hold (for example, three components instead of four), SIMD efficiencies are compromised.

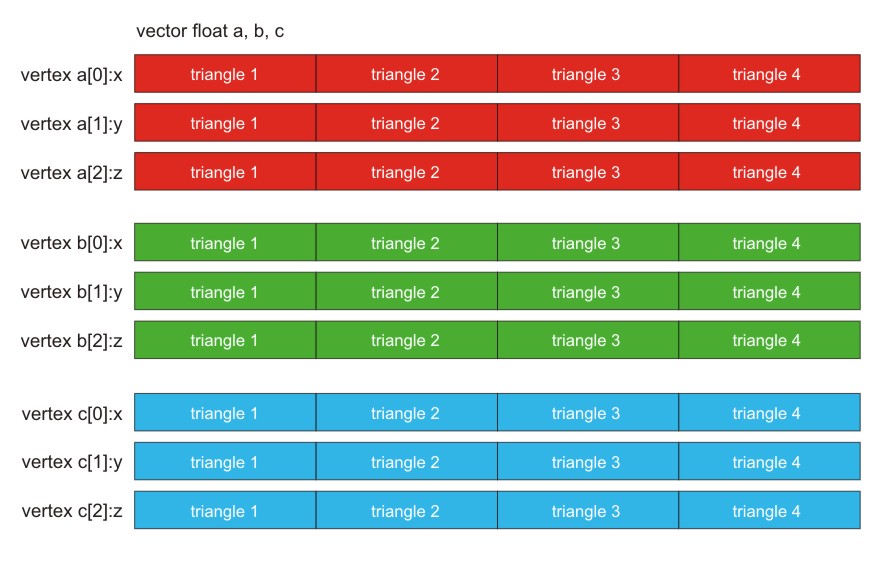
Another method of organizing data in SIMD vectors is a structure of arrays (SOA). Here, each corresponding data value for each vertex is stored in a corresponding location in a set of vectors. Think of the data as if it were scalar, and the vectors are populated with independent data across the vector. This is different from the previous example, where the four values of each vertex are stored in one vector. Figure 3 shows the use of SIMD vectors to represent the x, y, z vertices for four triangles. Not only are the data types the same across the vector, but now their data interpretation is the same. Depending on the algorithm, software might execute more efficiently with this SIMD data organization than with the organization shown in Figure 2.

Figure 3. Structure-of-arrays data organization for four triangles

For further details about the SPU instructions, refer to these documents:

The SPU Instruction Set Architecture,
The SPU Assembly Language Specification.